Downloading the PanSTARRS DR1 Catalogue via CasJobs

Before you begin running SQL queries on the PanSTARRS DR1 Catalogue via the command-line you first need to download the casjobs.jar java archive file and a config file.

Installation of CasJobs Command-Line Util

First move the jar files to a location on your machine’s $PATH. For example:

cd ~/Downloads
mv casjobs.jar /usr/local/bin/

…

PanSTARRS DR1 lives in Space-Telescope archives (images and catalogues) and a list of the DR1 database tables and their corresponding schema can be found here. We want to extract the minimum information from these tables required to integrate the catalogue into the Sherlock crossmatch-catalogues database. The big three checkboxes we need to hit are:

1. Positions of sources
2. Magnitudes of sources
3. Star-galaxy separation metric(s) for each source

…

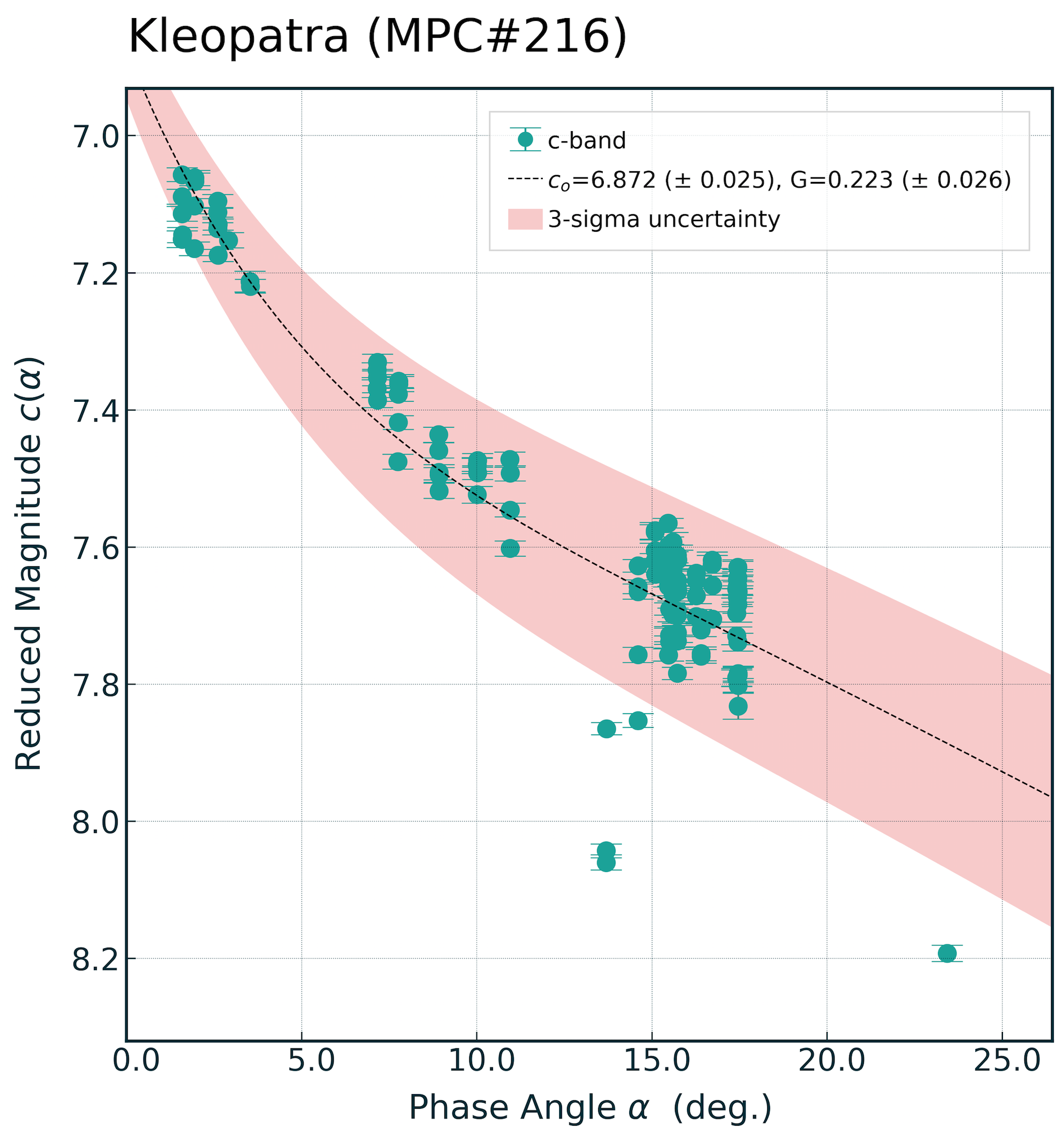
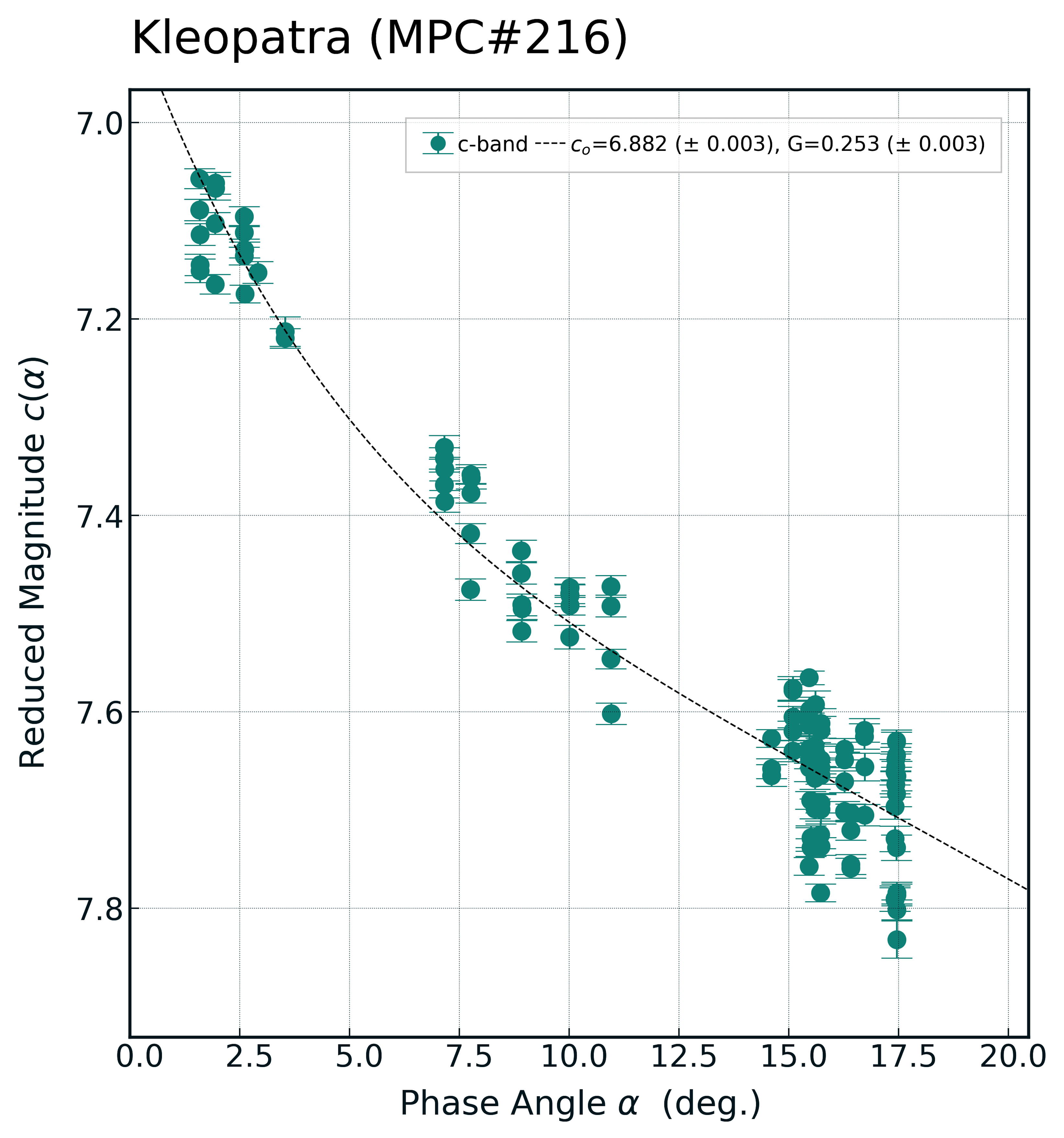
The reported errors in the ATLAS phase-curve fits appear to be coming out way too small. I’m calculating them as the square-root of the diagonals of the resulting co-variance matrix returned by scipy’s curve_fit.

perr = np.sqrt(np.diag(pcov))

Here’s what the covariance matrix looks like for Kleopatra:

[
    [ 0.00066722  0.00066133]
    [ 0.00066133  0.00073213]
]

Taking the sqrt of the diagonals gives the \(1\sigma\) errors in G and H: \(G_{err} = \sqrt{0.00066722}= 0.0258\), and \(H_{err} = \sqrt{0.00073213}= 0.0271\) …

The phase curve of a solar-system body reveals how its brightness changes as a function of its solar phase-angle, α ¹. The smaller the phase angle, the greater fraction of the asteroid’s lit surface can be seen from earth (or wherever the observer happens to be) and therefore the brighter its measured absolute magnitude. At a phase angle of 0^o the asteroid is fully illuminated.

As the asteroid orbits the sun it’s not only the asteroid’s phase-angle that changes but the sun-asteroid and asteroid-earth distances are also in constant flux. This has lead to the concept of a reduced magnitude which takes account of these distances to normalise the apparent magnitudes of asteroid. This reduced magnitude is now a function of only the asteroid’s solar phase-angle and is often represented as \(H(\alpha)\) to reflect this dependence. …

Stars saturate and bleed across many image pixels at the brighter end of the magnitude distribution. This can become an issue when it comes to correctly crossmatching and classifying these sources as image subtraction routines fail to difference the sources cleanly, resulting in a multiple artifacts being injected into the transient alert stream. Generally speaking, artefacts spread outward over a greater area from the source’s true centre the brighter the star is. …

OrbFit comes with four main programs Orbfit, Fitobs, Catpro and Bineph. In this tutorial we’re focusing on OrbFit’s title track, Orbfit, which can reportedly run in a non-interactive, batch-mode to perform a various operations on the orbits of asteroids and comets. However, in my experience so far orbfit neither works in non-interactive or batch-mode straight out of the box, but I’ve managed to generate a workflow that gets us part-way there. …